Liczba π z dokładnością do 200 miejsc po przecinku:
- π = 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196...
Symbol π wprowadził w 1706 roku William Jones w książce Synopsis Palmariorum Mathesos (π jest pierwszą literą greckiego słowa περίμετρον - perimetron, czyli obwód) a rozpowszechnił go później Leonhard Euler. Liczba π jest znana także jako stała Archimedesa lub ludolfina – tak została nazwana na cześć Ludolpha van Ceulena (obaj obliczyli przybliżone wartości π).
Niewymierność i przestępność liczby π
Liczba π jest liczbą niewymierną, co oznacza, że nie może być zapisana jako iloraz dwóch liczb całkowitych. Udowodnił to w roku 1761 Johann Heinrich Lambert. Co więcej, jest ona liczbą przestępną, co w 1882 roku wykazał Ferdinand Lindemann. Oznacza to, że nie istnieje wielomian o współczynnikach całkowitych, którego π jest pierwiastkiem. W rezultacie nie jest możliwe zapisanie π za pomocą skończonego zapisu złożonego z liczb całkowitych, działań arytmetycznych, ułamków oraz potęg i pierwiastków.
To ostatecznie rozstrzyga, że niemożliwa jest klasyczna konstrukcja (wyłącznie przy pomocy linijki i cyrkla) kwadratu o powierzchni równej powierzchni danego koła, gdyż współrzędne wszystkich punktów, które mogą być skonstruowane w taki sposób, należą do zbioru liczb nazywanych liczbami algebraicznymi. Problem ten zwany jest kwadraturą koła i choć nie ma on ścisłego rozwiązania, to istnieją konstrukcje przybliżone. Powiązanym, również niemożliwym do rozwiązania problemem, jest problem rektyfikacji okręgu, do którego również istnieją konstrukcje przybliżone, z których za jedną z najprostszych uchodzi konstrukcja Adama Adamandego Kochańskiego.
Dowód niewymierności π
Dowód przez sprowadzenie do sprzeczności.
Zakładamy, że 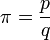 gdzie
gdzie  .
.
Ustalamy ciąg 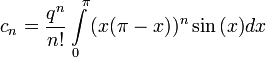
Można wykazać, że:
Oznaczać to będzie, że przyjęte założenie 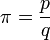 prowadzi
do sprzeczności, gdyż ciąg liczb całkowitych dodatnich nie może być zbieżny do
liczby 0.
prowadzi
do sprzeczności, gdyż ciąg liczb całkowitych dodatnich nie może być zbieżny do
liczby 0.
Często występujące przekształcenia π
Najpopularniejsze aproksymacje wartości π
Liczne wzory pozwalające wyliczać π z dowolną dokładnością podane są na końcu artykułu. W praktyce posługujemy się przybliżonymi wartościami 3,14 lub 22/7, rzadko kiedy trzeba korzystać z przybliżeń dokładniejszych: 3,1416 lub 3,14159 albo w postaci ułamka zwykłego 355/113 lub 52163/16604 (dwa ostatnie ułamki są równe π z dokładnością do 6 miejsc po przecinku).
Historia obliczeń wartości π
Z liczbą π, jakkolwiek pojawia się ona w wielu wzorach z różnych dziedzin (włączając w to nawet fizykę kwantową), ludzie zetknęli się już w starożytności, zauważając, że stosunek obwodu koła do jego średnicy jest wartością stałą. Babilończycy przyjmowali, że jest on równy w przybliżeniu 3.
Pierwsze źródła świadczące o świadomym korzystaniu z własności liczby π pochodzą ze starożytnego Babilonu. Na jednej z kamiennych tablic, datowanej na lata 1900-1680 p.n.e. pojawia się opis wartości obwodu koła o średnicy 1, przybliżony przez wartość 3,125.
Na pochodzącym sprzed 1650 r.
p.n.e. egipskim papirusie
Rhinda, autorstwa skryby (według niektórych źródeł tylko kopisty oryginału)
króla Ahmesa zatytułowanym Wprowadzenie
do wiedzy o wszystkich istniejących rzeczach można
znaleźć rozwiązania zadań matematycznych zawierające m.in. odniesienia do
wartości liczby π, przybliżanej wartością 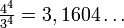
Podejście starożytnych uczonych do matematyki, w szczególności do liczby π było ściśle użytkowe, nie stosowano właściwie żadnej abstrakcji, a reguły matematyczne opisywane były prostymi przykładami użytkowymi, niezbędnymi w architekturze czy księgowości.
W Biblijnej Drugiej Księdze Kronik (Biblia Tysiąclecia, rozdział 4, werset 2) pochodzące z V - IV w. p.n.e. można znaleźć słowa:
-
- Następnie sporządził odlew okrągłego "morza" o średnicy dziesięciu łokci, o wysokości pięciu łokci i o obwodzie trzydziestu łokci.
Z opisu tego wynika, iż wykonawca owego "morza" przyjął oszacowanie π = 3.
Archimedes, będący prawdopodobnie pierwszym matematykiem badającym
dokładniej własności liczby
π w III
w. p.n.e. oszacował ją z
dokładnością do dwóch miejsc po przecinku. Użył do tego metody bazującej na
zależnościach geometrycznych, metody pozwalającą oszacowywać π z (teoretycznie)
dowolną dokładnością, przez następne wieki była metodą najlepszą, często
niezależnie od prac Archimedesa wykorzystywaną przez późniejszych matematyków.
Wynikiem jego pracy było podanie przedziału, w jakim mieści się liczba π: 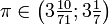 .
Archimedes uzyskał ten wynik wyznaczając długości boków dwóch 96-kątów foremnych
- opisanego na okręgu i wpisanego w ten sam okrąg. Następnie obliczył średnią
arytmetyczną obwodów tych wielokątów, otrzymując przybliżenie długości okręgu.
Obliczenia były bardzo żmudne i czasochłonne. Mimo wielkich wysiłków
Archimedesowi nie udało się dokonać analogicznych obliczeń dla 192-kątów, co
pozwoliłoby mu wyznaczyć wartość ludolfiny z jeszcze większą dokładnością.
.
Archimedes uzyskał ten wynik wyznaczając długości boków dwóch 96-kątów foremnych
- opisanego na okręgu i wpisanego w ten sam okrąg. Następnie obliczył średnią
arytmetyczną obwodów tych wielokątów, otrzymując przybliżenie długości okręgu.
Obliczenia były bardzo żmudne i czasochłonne. Mimo wielkich wysiłków
Archimedesowi nie udało się dokonać analogicznych obliczeń dla 192-kątów, co
pozwoliłoby mu wyznaczyć wartość ludolfiny z jeszcze większą dokładnością.
Liu Hui, chiński matematyk żyjący w III wieku naszej ery, metodą Archimedesa dla wieloboków o 3072 bokach ustalił przybliżoną wartość liczby π na 3,1415.
Zu Chongzhi, chiński cesarski astronom około 500 roku
n.e. podał dwa przybliżenia liczby π - wcześniejsze - 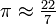 ,
oraz późniejsze, wynoszące
,
oraz późniejsze, wynoszące 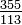 ,
które do XV
wieku było najlepszym znanym
ludzkości przybliżeniem wartości liczby π (na szczególną uwagę zasługuje łatwość
jego zapamiętania: 11-33-55). Wartości te zanotowano w pochodzących z tego
okresu kronikach dworskich. Użył on metody Archimedesa, lecz najprawdopodobniej
nie miał dostępu do jego prac.
,
które do XV
wieku było najlepszym znanym
ludzkości przybliżeniem wartości liczby π (na szczególną uwagę zasługuje łatwość
jego zapamiętania: 11-33-55). Wartości te zanotowano w pochodzących z tego
okresu kronikach dworskich. Użył on metody Archimedesa, lecz najprawdopodobniej
nie miał dostępu do jego prac.
Brahmagupta, hinduski matematyk, sto lat później (około 600 r.n.e.),
podał inne przybliżenie wartości π -  ,
stosując własności12,24,48 i 96-boków,
których długości obwodów wynosiły odpowiednio
,
stosując własności12,24,48 i 96-boków,
których długości obwodów wynosiły odpowiednio  .
W rzeczywistości
.
W rzeczywistości 
W 1400 roku hinduski matematyk Madhava jako pierwszy w historii do obliczenia wartości π użył ciągów nieskończonych. W istocie odkrył on wzór, do którego Leibniz i Gregory (autorstwo przypisuje się obu) doszli w 1674. Natomiast pierwszym z Europejczyków, który użył metody aproksymacji π przy pomocy ciągów nieskończonych był John Wallis, który w 1656 roku w dziele Arithmetica infinitorum podał bardzo zgrabny - aczkolwiek niezbyt użyteczny - wzór na π. Od tego czasu do obliczania wartości π zaczęto używać ciągów nieskończonych - zazwyczaj przy pomocy rozwinięcia funkcjiarcus sinus lub arcus tangens w szereg potęgowy. Mimo to w 1596 roku Ludolph van Ceulen podał przybliżenie π z dokładnością do 35. miejsca po przecinku, używając do tego metody Archimedesa. Obliczenia prowadził przez całe życie.
Ludolph van Ceulen stosując metodę Archimedesa oblicza wartość π z dokładnością do 20 miejsc po przecinku, publikując wynik w dziele Van den Circkel (1596). Według biografów Ceulen większość swojego życia poświęcił próbom coraz lepszego przybliżenia π, zwanej niekiedy od jego imienia Ludolfiną, pod koniec życia podając π z dokładnością do 35 miejsc po przecinku (użył do tego wieloboku o 262 bokach!) - wartość ta została wyryta na jego płycie nagrobkowej.
Z biegiem lat uzyskiwano coraz lepsze przybliżenia wartości π sięgające kilkuset miejsc po przecinku. W 1853 William Rutherford podał liczbę Pi z dokładnością 440 miejsc po przecinku. Rekordzistą w ręcznych obliczeniach liczby Pi jest William Shanks, któremu w 1874 udało się uzyskać 707 miejsc po przecinku. Zajęło mu to 15 lat. Później okazało się, że 180 ostatnich cyfr obliczył błędnie (wynik, który uznano za prawidłowy uwzględnia 527 miejsc po przecinku). W 1946 roku Ferguson podał wartość π do 620. miejsca po przecinku. W końcowych obliczeniach wspomagał się już kalkulatorem. Od 1949, kiedy to przy pomocy komputera ENIAC obliczono 2037 miejsc po przecinku, dokładniejsze aproksymacje liczby π uzyskiwano już tylko przy użyciu komputerów. We wrześniu 1999 roku obliczono π z dokładnością 2,0615·1011 miejsc po przecinku. Dokonał tego Takahasi przy pomocy komputera HITACHI SR8000.
31.12.2009 Fabrice Bellard ogłosił, że udało mu się obliczyć π z dokładnością do 2 699 999 990 000 miejsc po przecinku. Obliczenia ze sprawdzeniem zajęły 131 dni, a do obliczeń użyto komputera z procesorem Intel Core i7 (2,93 GHz) i 6 GB RAM. Sam zapis dziesiętny liczby zajmuje około 1137 GB.
W roku 2010 obliczono 2 000 000 000 000 000 cyfrę liczby pi i wynosi ona zero. Obliczenia trwały 23 dni.
Wzory do obliczania liczby π
- Powierzchnia koła jednostkowego:
- Obwód okręgu jednostkowego:
- François Viète, 1593:
- Leibniz:
- Wallis:
Powyższe metody są wolno zbieżne. Do szybkich obliczeń komputerowych stosuje się przybliżenie wynikające z tożsamości:
Funkcję arcus tangens należy rozwinąć w szereg Taylora. Twórcą tej formuły jest angielski matematyk John Machin (1680—1751).
Szybkozbieżnych formuł postaci :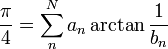 pojawiło
się więcej, m.in:
pojawiło
się więcej, m.in:
- K. Takano (1982):
- F. C. W. Störmer (1896):
- S. Klingenstierna (1730):
- Newton:
- Ramanujan:
- David Chudnovsky i Gregory Chudnovsky:
- Bailey-Borwein-Plouffe Bailey web page (1997)
Istnieją także rozwinięcia w ułamki łańcuchowe:
- W. Brouncker (ok. 1600)
- L. Euler (ok. 1755)
Kultura π

Liczba π ma swoich licznych wielbicieli. Obchodzą oni dzień π (14 marca) (amerykański sposób zapisu daty 3.14) oraz dzień aproksymacji π (22 lipca) (europejski sposób zapisu daty 22/7=~3.1428).
Tworzone są też wierszyki i opowiadania, w których długość każdego kolejnego słowa jest równa kolejnej cyfrze w rozwinięciu dziesiętnym liczby π.
Niemcom w zapamiętaniu aproksymacji π uzyskanej przez van Ceulena może być pomocny wiersz napisany przez Clemensa Brentano, który jest przypuszczalnie pierwszym tego typu tekstem:
-
Nie, o Gott, o guter, verliehst Du meinem Hirne die Kraft mächtige Zahlreihn
dauernd verkettet bis in die spaetere Zeit getreu zu merken. Drum hab ich
Ludolph mir zu Lettern umgeprägt.
- Nigdy, o dobry Boże, nie użyczysz mi mocy spamiętania po wsze czasy potężnego, ze sobą trwale sprzężonego szeregu cyfr. Dlatego przyswoiłem sobie ludolfinę w słowach. (przekład Witolda Rybczyńskiego)
Pierwszym polskim wierszem tego typu jest nieco toporny wiersz Kazimierza Cwojdzińskiego z 1930 roku, zamieszczony w październikowym wydaniu czasopisma Parametr, poświęconemu nauczaniu matematyki. Należy jednak pamiętać, że tekst powstał przed reformą ortografii z 1936 roku. Wtedy pisano nie ma w znaczeniu 'nie posiada' i niema w znaczeniu 'nie jest'.
- Kuć i orać w dzień zawzięcie,
- Bo plonów niema bez trudu!
- Złocisty szczęścia okręcie,
- Kołyszesz...
- Kuć! My nie czekajmy cudu.
-
Robota to potęga ludu!
Rymowany wiersz, w którym liczba liter w kolejnych wyrazach odpowiada rozwinięciu dziesiętnemu liczby pi do 20 miejsca po przecinku:
-
Kto w mgłę i słotę wagarować ma ochotę?
-
Chyba ten który ogniście zakochany, odziany wytwornie
-
Gna do nóg Bogdanki paść kornie
Inne przykłady:
-
Jaś o kole z werwą dyskutuje
- bo
dobrze temat ten czuje
-
zastąpił ludolfinę słowami wierszyka
- czy Ty już odgadłeś, skąd zmiana ta wynika ?
- Oto i wiem i pomnę doskonale...
- Kto z woli i myśli zapragnie Pi spisać cyfry, ten zdoła.
Oto limeryk opublikowany kiedyś w miesięczniku Delta:
- Raz w maju, w drugą niedzielę
- Pi liczył cyfry pan Felek.
- Pomnożył, wysumował,
- Cyferki zanotował,
- Ale ma ich niewiele...
Są nawet wiersze białe:
- Źle w mgle i snach bolejącym do wiedzy progu iść.
Kolejny, dłuższy przykład, w formie inwokacji do bogini pamięci (myślnik po 'pauza' zastępuje zero):
- Daj, o pani, o boska Mnemozyno, pi liczbę, którą też zowią ponętnie Ludolfiną, pamięci przekazać tak, by jej dowolnie oraz szybko do pomocy użyć; gdy się problemu nie da inaczej rozwiązać, pauza − to zastąpić liczbami.
Najbardziej znany przykład angielski jest autorstwa sir Jamesa Jeansa:
-
How I want a drink, alcoholic of course, after the heavy lectures involving
quantum mechanics!
- Jakże chciałbym się napić, czegoś mocnego oczywiście, po trudnych wykładach dotyczących mechaniki kwantowej!
Popularny jest także następujący wierszyk:
-
How I wish I could recollect Pi easily today!
- Jakże bym chciał dzisiaj łatwo przypomnieć sobie Pi!
Popularny jest również polski wierszyk:
- Był i jest i wieki chwalonym ów będzie który kół obwód średnicą wymierzył
Liczba π była inspiracją wielu artystów i reżyserów. Darren Aronofsky poruszył jej temat w swoim filmie Pi. W literaturze Pi jest imieniem bohatera powieści Yanna Martela-"Życie Pi" oraz tematem jednego z wierszy Wisławy Szymborskiej. Rozwinięcie binarne liczby π (jako zaszyfrowana informacja dotycząca sensu wszechświata) odgrywa kluczową rolę w zakończeniu znanej powieści s-f "Kontakt" Carla Sagana. Fascynacja π jako kluczem czy ważnym elementem "wiedzy tajemnej" bywa obecna w wielu paranaukowych czy ezoterycznych sektach i stowarzyszeniach, poczynając od XVIII w.
W latach 80. XX w. w Polsce emitowany był telewizyjny program edukacyjny przeznaczony dla dzieci i młodzieży pt. Przybysze z Matplanety, w którym jednym z bohaterów był nieśmiały i tchórzliwy Pi.
Księga Guinnessa zawiera listę ludzi którzy zapamiętali najwięcej cyfr liczby Pi. Należy do nich np. Rajan Mahadevan (40 000 zapamiętanych cyfr),Daniel Tammet.
Znak π[edytuj]
Znak π jest oznaczeniem matematycznym wywodzącym się z litery alfabetu greckiego powszechnie używanym do oznaczenia liczby, której wartością jest stosunek długości obwodu koła do długości jego średnicy.
Jej pierwszego utożsamienia z
wartością  dokonał
w dziele Synopsis Palmariorum
Matheseos (1706) William
Jones, walijski matematyk i pisarz. Oznaczenie to nie zdobyło uznania ani
rozgłosu wśród matematyków, do czasu użycia go przez Leonarda
Eulera w 1737 roku,
w dziele Analiza, chociaż
można znaleźć je we wcześniejszych pracach matematyków Williama
Oughtreda, Isaaca
Barrowa i Davida
Gregory'ego. Oznaczenie pochodzi najpewniej ze związku wartości pi i
długości obwodu, którego grecka nazwa to περιμετρον.
dokonał
w dziele Synopsis Palmariorum
Matheseos (1706) William
Jones, walijski matematyk i pisarz. Oznaczenie to nie zdobyło uznania ani
rozgłosu wśród matematyków, do czasu użycia go przez Leonarda
Eulera w 1737 roku,
w dziele Analiza, chociaż
można znaleźć je we wcześniejszych pracach matematyków Williama
Oughtreda, Isaaca
Barrowa i Davida
Gregory'ego. Oznaczenie pochodzi najpewniej ze związku wartości pi i
długości obwodu, którego grecka nazwa to περιμετρον.
W Introductio in Analysin Infinitorum (1748) Euler pisze:
-
- Satis liquet Peripheriam hujus Circuli in numeris rationalibus exacte exprimi non posse, per approximationes autem inventa est .. esse = 3,14159 [itd do 128 cyfr], pro quo numero, brevitatis ergo, scribam pi, ita ut sit π = Semicircumferentiae Circuli, cujus Radius = 1, seu pi erit longitudo Arcus 180 graduum.
Prawdopodnie znaczący wpływ na popularyzację symbolu π miało jego pojawienie się w Mathematical Tables (1742) Henry'ego Sherwina.
Porzucone oznaczenia
- Euler w wydanym przed Analizą dziele De summis serierum reciprocarum (1734) używa oznaczenia p dla Π. Co ciekawe, używa on też tego oznaczenia w napisanym już po wydaniu Analizy liście do Jamesa Stirlinga z 16 kwietnia 1738.
- W liście, napisanym do Eulera w 1739 roku przez Johanna Bernoulli, używa on oznaczenia c dla liczby pi, jednak już w następnym liście do Eulera, z początku 1740 stosuje on oznaczenie π.
Niektóre wzory zawierające 
Geometria
-
 - obwód okręgu o
promieniu r
- obwód okręgu o
promieniu r -
 - pole elipsy o
półosiach równych a i b
- pole elipsy o
półosiach równych a i b -
 - objętość n wymiarowej kuli o
promieniu r
- objętość n wymiarowej kuli o
promieniu r -
 - powierzchnia kuli
o promieniu r
- powierzchnia kuli
o promieniu r - Miara łukowa kąta półpełnego równa jest π radianów
- V = πr2H - objętość walca
Analiza matematyczna
-
 (Euler)
(Euler) -
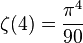
-
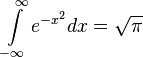 (rozkład
normalny)
(rozkład
normalny) -
 (wzór
Stirlinga)
(wzór
Stirlinga) -
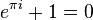 (Wzór
Eulera, nazywany również najpiękniejszym
wzorem matematyki)
(Wzór
Eulera, nazywany również najpiękniejszym
wzorem matematyki) -

Teoria liczb
- Prawdopodobieństwo tego, że dwie losowo
wybrane liczby całkowite są liczbami
względnie pierwszymi wynosi
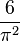 .
. - Średnia liczba sposobów na zapisanie liczby
naturalnej jako sumy dwóch
liczb całkowitych, których pierwiastek też jest liczbą całkowitą, wynosi
 .
.
W powyższych przypadkach prawdopodobieństwo i średnią rozpatruje się w sensie granicznym np: rozważamy prawdopodobieństwo dla zbioru liczb {1, 2, 3,…, N} a następnie obliczamy granicę przy N dążącym do nieskończoności.


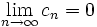
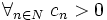

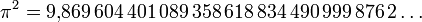
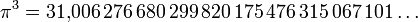



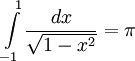
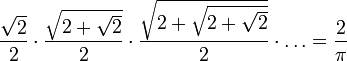
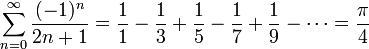
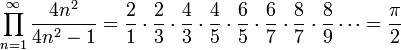
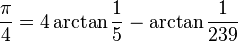
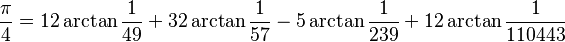



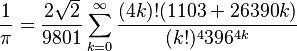
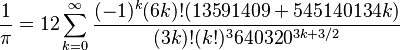
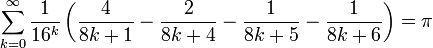


.jpg)
